I logaritmi
La natura sembra prediligere i logaritmi. E’ un fatto che molti fenomeni naturali trovino descrizione chiara e sintetica proprio quando vengono formulati facendo uso dei logaritmi. Prima di mostrare qualche esempio cerchiamo di capire cosa sono i logaritmi utilizzando lo stesso ragionamento che portò alla loro scoperta.
I logaritmi vennero scoperti da uno scozzese di nobile famiglia vissuto a cavallo fra il sedicesimo e il diciassettesimo secolo in pieno scisma anglicano. Si chiamava John Napier, ma è meglio noto con il nome latinizzato di Nepero. Egli aveva mostrato fin da bambino una spiccata attitudine per la matematica, che tuttavia non sfruttò adeguatamente preferendo dedicarsi agli studi di teologia ai quali si applicò con grande profitto. Mentre era ancora studente aderì alla associazione per la riforma religiosa e in seguito fu esponente di spicco del movimento politico protestante, fortemente critico nei confronti del cattolicesimo. Passato il periodo dell’infatuazione mistica si dedicò con maggiore assiduità ai problemi della matematica e della fisica applicata progettando, fra l’altro, macchine da guerra non molto dissimili da quelle che verranno costruite e utilizzate, tre secoli più tardi, in occasione del primo conflitto mondiale.
I LOGARITMI FACILITANO I CALCOLI
Il nome di Nepero resta tuttavia legato all’invenzione dei logaritmi ai quali lo scienziato arrivò notando una sorprendente corrispondenza fra i termini di alcune progressioni numeriche: queste non sono altro che successioni di numeri ordinati secondo una determinata legge. Consideriamo quindi anche noi due particolari progressioni numeriche e precisamente: 0, 2, 4, 6, 8, 10, 12, 14, 16 e 1, 4, 16, 64, 256, 1.024, 4.096, 16.384, 65.536. La prima serie di numeri che abbiamo scritto si chiama progressione aritmetica ed è caratterizzata dal fatto che ciascun termine si ottiene aggiungendo 2 al precedente. La seconda serie di numeri si chiama progressione geometrica ed è caratterizzata dal fatto che ciascun termine si ottiene dal precedente moltiplicandolo per 4. In generale, in una progressione aritmetica è sempre costante la differenza fra ciascun termine (escluso il primo) e il suo precedente e in una progressione geometrica è sempre costante il quoziente fra ciascun termine (escluso il primo) e il suo precedente. Questi valori costanti si chiamano ragione delle rispettive progressioni.
Prendiamo ora due termini qualsiasi della prima progressione scritta sopra, ad esempio il 4 e il 12, sistemati rispettivamente al 3° e al 7° posto e sommiamoli; si ottiene 16, un numero che occupa il 9° posto della serie. Se adesso consideriamo i termini che nella seconda progressione si trovano sistemati anch’essi al 3° e al 7° posto, cioè il 16 e il 4.096 e li moltiplichiamo otteniamo un numero, 65.536, che occupa lo stesso posto, il nono, che nella prima progressione occupava la somma.
Facciamo un altro esempio. Prendiamo il 6 che è sistemato al 4° posto della prima progressione e sottraiamolo dal 14 che sta all’8° posto; otteniamo 8, un numero che occupa il 5° posto della serie. Passiamo ora alla seconda progressione e dividiamo i due numeri sistemati, come i precedenti, rispettivamente all’ottavo e al quarto posto cioè 16.384 e 64; otteniamo 256, cioè un numero che ancora una volta occupa il 5° posto, esattamente dove si trovava l’8 (il risultato della sottrazione) all’interno della progressione aritmetica.
Il procedimento apparentemente laborioso che abbiamo illustrato serve a chiarire che le operazioni di moltiplicazione e di divisione, più difficili da eseguire, possono essere sostituite da quelle di addizione e sottrazione concettualmente più facili. Ebbene, i logaritmi sono proprio questo: servono a semplificare i calcoli. Vediamo quindi di definire con maggiore precisione questi nuovi strumenti di calcolo che abbiamo appena individuato.
Per farlo dobbiamo prima riscrivere la progressione geometrica utilizzata sopra in modo diverso e cioè come segue: 20, 22, 24, 26, 28, 210, 212, 214, 216. Ciascun elemento della serie ora appare espresso sotto forma di potenza. Una potenza, come sappiamo, è costituita da un numero chiamato base (il 2 nel nostro esempio) elevato ad un altro numero chiamato esponente. E’ facile verificare che i termini della progressione rappresentati sotto forma di potenze corrispondono a quelli della progressione geometrica scritta sopra: 20 = 1, 22 = 4, 24 = 16, 26 = 64 e così via. Si noti inoltre che gli esponenti dei termini della nuova progressione (0, 2, 4, 6 ecc.) sono gli stessi numeri che compaiono nella progressione aritmetica scritta all’inizio.
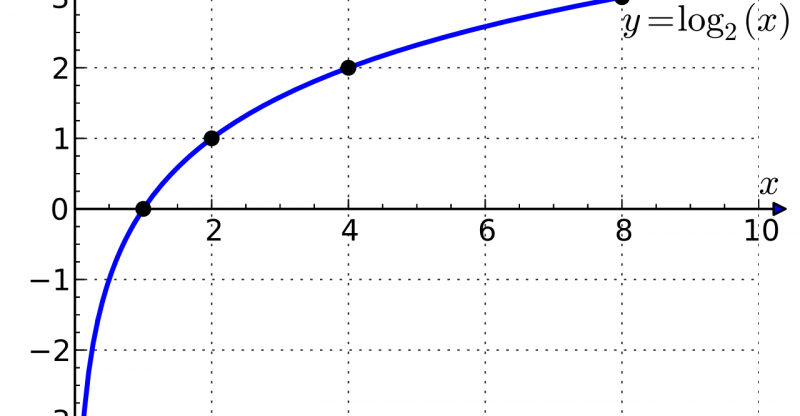
Ora possiamo dare la definizione completa di logaritmo: “Il logaritmo di un numero in una certa base è l’esponente a cui bisogna innalzare la base per ottenere il numero stesso”. Ad esempio, il logaritmo di 100 in base 10 è 2 perché 10² fa 100. In simboli il nostro logaritmo si scrive nel modo seguente: log10100 = 2. Si noti che il logaritmo è semplicemente l’esponente di una potenza e che le due eguaglianze log10100 = 2 e 102 = 100 sono equivalenti.
Abbiamo detto che i logaritmi furono utilizzati originariamente per semplificare i calcoli numerici che oggi è possibile eseguire facilmente con le calcolatrici tascabili e quindi hanno perso gran parte della loro originaria funzione. I logaritmi tuttavia attualmente trovano ancora impiego e applicazione in tante discipline quali la biologia, l’astronomia, le scienze della terra e nelle operazioni finanziarie.
Per comprendere in che modo i logaritmi sono in grado di rendere più semplici i calcoli basta notare che esprimendo i numeri sotto forma di potenze la moltiplicazione e la divisione si riducono a semplici somme e sottrazione di esponenti (ad esempio, la moltiplicazione di 10.000 per 1.000 si trasforma semplicemente in 104 · 103 = 104+3 = 107) e l’elevamento a potenza e l’estrazione di radice diventano una semplice operazione di moltiplicazione e di divisione degli esponenti (ad esempio la radice cubica di 1.000.000 è 106/3 = 102.
Non tutti i numeri, però, possono essere espressi sotto forma di potenze in modo immediato e semplice come avviene per i multipli del 10. Per esprimere un numero qualsiasi, ad esempio 132, sotto forma di potenza del 10, bisognerebbe andare alla ricerca di un numero frazionario (compreso fra il 2 e il 3) da porgli ad esponente. Il calcolo di questo numero non è cosa semplice e se dovessimo farlo su tutti i numeri prima di eseguire (in modo semplice) ad esempio una moltiplicazione, usando gli esponenti delle potenze, il guadagno di tempo non ci sarebbe più e converrebbe operare in modo tradizionale.
Ma prima lo scozzese Nepero, e successivamente l’inglese Briggs fecero la fatica di calcolare i logaritmi di molti numeri. Henry Briggs (1561-1631), amico ed estimatore di Nepero, si prese la briga di calcolare i logaritmi in base 10 dei numeri da 1 a 20.000 e da 90.000 a 100.000 con quattordici cifre decimali, un lavoro immane di cui approfittarono i suoi contemporanei e gli immediati successori, i quali si avvalsero dei logaritmi per le loro ricerche con risultati sorprendenti. Keplero, ad esempio, se ne servì per scoprire le sue famose leggi astronomiche.
Come si è visto, i logaritmi consentono, per così dire, di “abbassare di grado” le operazioni sui numeri: elevamento a potenza ed estrazione di radice vengono sostituite da moltiplicazione e divisione e queste ultime da addizione e sottrazione; è chiaro che il vantaggio di un tale procedimento sarà tanto maggiore quanto più complicati saranno i calcoli. Ovviamente i logaritmi non sono applicabili alle operazioni di addizioni e sottrazione.
FUNZIONE ESPONENZIALE E SOVRAPPOPOLAZIONE
Ogni processo di accrescimento può essere lineare o esponenziale. Si dice che una grandezza cresce linearmente quando ad intervalli di tempo uguali corrispondono incrementi uguali: così, ad esempio, è lineare l’incremento dei risparmi di un bambino a cui la mamma, ogni anno, mette da parte un milione di lire: dopo un anno il bambino si troverà con un milione di lire di risparmi, dopo due anni con due milioni, dopo tre anni con tre e così via.
Si dice invece che una grandezza cresce esponenzialmente allorché ad intervalli di tempo uguali corrispondono incrementi pari ad una frazione costante del totale. Se un’altra mamma meno generosa ma più concreta, invece che mettere ogni anno un milione nel salvadanaio del figlio ne avesse messo uno solo ma in banca al tasso di interesse ad esempio del 7% annuo, alla fine dell’anno il bambino avrebbe un milione e settantamila lire. L’anno successivo, l’interesse del 7% verrebbe calcolato su 1.070.000 lire e produrrebbe altre 75.000 lire circa di interesse che si andrebbero ad aggiungere alla somma già posseduta. L’anno ancora successivo l’interesse verrebbe quindi calcolato su una cifra nuovamente più alta. Ora è facile comprendere che quanto maggiore è la somma depositata sul conto tanto più denaro verrà aggiunto ogni anno come interesse; ma quanto più se ne aggiunge tanto più ve ne sarà nel conto l’anno successivo e quindi ancora più se ne aggiungerà come interesse. La caratteristica delle crescite esponenziali è proprio questa: più è grande la quantità di cui si dispone, più essa si accresce. Se la quantità è piccola aumenta poco, se è media aumenta moderatamente, se è grande aumenta molto.
I processi di crescita esponenziale sono assai comuni in campo finanziario, in biologia e in tanti altri settori del sapere, dove a volte possono produrre conseguenze sorprendenti.
Un modo per illustrare l’estrema rapidità con la quale una crescita esponenziale porta ad approssimarsi ad un valore prefissato è quella di fare ricorso ad un indovinello per bambini. L’indovinello è il seguente. Immaginiamo di avere un laghetto al centro del quale cresce una ninfea che ogni giorno raddoppia le proprie dimensioni: se la pianta potesse svilupparsi liberamente, dopo 30 giorni coprirebbe completamente il lago soffocando tutte le altre forme di vita. Ora, se si decidesse di tagliare la ninfea quando le sue foglie hanno coperto metà del lago in modo da salvarlo da morte sicura in quale giorno si dovrebbe intervenire? La risposta è al 29° giorno, cioè vi sarebbe un solo giorno di tempo per rimediare ad una situazione che il giorno dopo diventerebbe irreparabile. Il risultato è sorprendente soprattutto se si riflette sul fatto che il 25° giorno era coperto appena poco più del 3% del lago: nelle crescite di tipo esponenziale all’inizio le cose vanno piano poi accelerano in modo impressionante.
La crescita esponenziale viene spesso espressa efficacemente attraverso il cosiddetto “tempo di raddoppiamento”, che è il tempo necessario affinché una grandezza raddoppi il proprio valore (incremento del 100%). Nel caso della ninfea che abbiamo appena esaminato il tempo di raddoppiamento è di un giorno; per la somma di denaro depositata in banca all’interesse del 7% annuo il tempo di raddoppiamento è pari a 10 anni circa. Non è difficile calcolare il tempo di raddoppiamento di una crescita esponenziale se si conosce il tasso di crescita: esso, in anni, è approssimativamente uguale a 70 diviso per il valore percentuale del tasso stesso.
Secondo i calcoli del Fondo per la popolazione delle Nazioni Unite il 12 ottobre 1999 gli abitanti della Terra sono diventati 6 miliardi. In realtà nessuno li ha contati: il numero è frutto di estrapolazioni statistiche e valutazioni di vario genere e tuttavia non dovrebbe essere molto lontano dal vero. Pertanto, giorno più o giorno meno, ormai ci siamo: gli abitanti del pianeta con l’ingresso nel nuovo millennio hanno raggiunto e superato quota 6 miliardi e si calcola che crescano al ritmo di 1,5% all’anno, cioè ogni anno aumentano di novanta milioni di unità (ma in seguito, come vedremo subito, l’aumento sarà sempre più consistente). Si tratta di un numero enorme: basta pensare che se si volesse dare una casa dignitosa ai nuovi arrivi si dovrebbe costruire tutti i giorni una città grande come Trieste.
Se la popolazione mondiale continuasse a salire a questo ritmo, nel 2047 sarebbe il doppio di oggi (70:1,5 = 47), e fra meno di 700 anni arriverebbe a 150.000 miliardi, cioè vi sarebbe un uomo ogni metro quadrato di superficie terrestre. E’ evidente che la popolazione non potrà continuare a crescere a questo ritmo all’infinito perché la Terra è di dimensioni finite e su di essa non può esserci niente che diventa infinitamente grande. La Terra non può quindi produrre alimenti in quantità illimitate né tanto meno ospitare uomini in numero illimitato.
Ora, se volessimo rappresentare con un grafico la crescita della popolazione mondiale di questi ultimi secoli, ponendo sull’asse orizzontale di un piano cartesiano i tempi e su quello verticale il numero degli uomini, scelte opportunamente le unità di misura, si otterrebbe una curva che si innalza quasi verticalmente al passare del tempo. Questo tipo di curva prende il nome di curva esponenziale, o anche, a causa della sua forma, “curva J” ed è la rappresentazione grafica di quello che i matematici chiamano “funzione esponenziale”.
Con il termine di funzione si intende una grandezza che dipende da un’altra grandezza. Il numero degli abitanti del nostro pianeta dipende dal tempo, quindi possiamo dire che questo numero è funzione del tempo che passa. In verità, quando una grandezza dipende da un’altra grandezza, si può considerare indifferentemente la prima funzione della seconda o viceversa. Si è convenuto quindi di chiamare funzione (o variabile dipendente) la grandezza che costituisce l’oggetto di studio e variabile indipendente quella che fa la parte accessoria. Quando consideriamo il numero degli abitanti che cresce con il passare del tempo, lo scopo non è quello di misurare come passa il tempo per mezzo del numero degli abitanti del pianeta, bensì di misurare il numero degli abitanti con l’aiuto del tempo. Quindi, in questo caso, chiameremo variabile dipendente il numero degli abitanti e variabile indipendente il tempo. E’ consuetudine indicare con y la variabile dipendente e con x la variabile indipendente; in simboli si scrive così: y = f(x) e si legge y è uguale a una funzione di x. Se x è l’esponente di un’espressione algebrica o anche semplicemente di un numero, la funzione diventa una funzione esponenziale. Ad esempio, y = 2x è una funzione esponenziale.
Nelle funzioni esponenziali (con base maggiore di 1) se il valore della x cresce lentamente la funzione intera cresce molto, ma molto più rapidamente: ad esempio, nella funzione y = 10x se x assume i valori successivi di 1, 2, 3, 4, ecc., la y assume i valori corrispondenti di 10, 100, 1.000, 10.000, ecc. Se la base è minore di 1 (ma maggiore di zero) la funzione diventa sempre più piccola a mano a mano che la x cresce: ad esempio nella funzione esponenziale y = 0,5x se x assume i valori successivi di 1, 2, 3, 4, ecc. la y diventa 0,50, 0,25, 0,12, 0,06, ecc.
L’INCERTEZZA DELLE PREVISIONI
L’uomo, in passato, ha conosciuto tassi locali di crescita della popolazione molto vari e irregolari. In alcuni momenti si sono verificati perfino casi di decremento demografico come ad esempio in occasione della peste nera del 1348 quando in pochi anni in Europa morì quasi un terzo della popolazione residente. In verità, specialmente per l’antichità, i dati sono molto incerti ma pare che fino a 2.000 anni fa i tassi di natalità e di mortalità siano stati in sostanziale equilibrio. Poi la popolazione ha cominciato a crescere ma lo ha fatto, fino ad un paio di secoli addietro, ad un ritmo talmente basso che nessuno si era accorto dell’incremento demografico in atto.
Non sappiamo con certezza quando sulla Terra sia comparso l’uomo anatomicamente moderno, cioè la nostra specie di Homo sapiens sapiens, ma possiamo fissare quella data a circa 100.000 anni fa, quando presumibilmente erano presenti pochi individui che vivevano cacciando e raccogliendo frutti, bacche e altri vegetali. Una prima valutazione della popolazione si può fare per il periodo in cui ebbero inizio l’agricoltura e l’addomesticazione degli animali, ossia circa 10.000 anni fa. Gli antropologi e gli storici hanno valutato in circa 8 milioni di unità la dimensione della popolazione in quel momento.
In 90.000 anni la popolazione del pianeta passò quindi da zero (o se si preferisce da due: Adamo ed Eva) a 8 milioni di individui con un incremento annuo estremamente ridotto (0,01 per mille). Dopo la diffusione dell’agricoltura l’incremento demografico aumentò passando da 0,01 per mille a 0,44 per mille e gli 8 milioni di uomini dell’8.000 a.C. divennero, nell’anno 1, circa 250 milioni. Dall’anno 1 al 1800 la popolazione del globo arrivò al miliardo di individui; da quella data prese avvio la straordinaria accelerazione moderna dell’incremento demografico.
Agli inizi del secolo scorso la popolazione era di poco più di un miliardo e mezzo di individui e raddoppiò entro il 1960 quando raggiunse i 3 miliardi. Poi, in quarant’anni, raddoppiò di nuovo raggiungendo i 6 miliardi attuali.
Il nostro pianeta ha visto il massimo tasso di accrescimento agli inizi degli anni Settanta del secolo scorso quando la popolazione mondiale ammontava a tre miliardi e mezzo di individui. A quel tempo l’incremento annuo era pari a 2,1% che corrispondeva a un tempo di raddoppiamento di 33 anni. Ad iniziare dalla rivoluzione industriale (seconda metà del XVIII secolo) e fino ad una trentina d’anni fa, non solo la popolazione mondiale è cresciuta esponenzialmente, ma è aumentato anche il tasso di crescita. Potremmo quindi dire che in quel periodo la crescita della popolazione è risultata iperesponenziale. Se si fosse continuato al ritmo di crescita degli anni Settanta oggi la popolazione mondiale sarebbe di 7 miliardi di persone invece che di 6.
Da quella data invece, soprattutto per il diffondersi nei paesi industrializzati delle pratiche anticoncezionali e per la politica del contenimento delle nascite operata in Cina, il tasso di incremento demografico è calato, ma non è calato il numero degli abitanti del pianeta né è calato il numero di quelli che si aggiungono annualmente ai presenti. Agli inizi degli anni ‘70 del secolo che si è appena concluso, con un tasso di incremento del 2,1%, si aggiungevano alla popolazione esistente (3,5 miliardi) meno di 75 milioni di nuovi individui all’anno, oggi, nonostante il calo del tasso di incremento dal 2,1% all’1,5% annuo, il numero di abitanti che va ad unirsi a quelli che già ci sono (6 miliardi) è di circa 90 milioni all’anno.
Non è la prima volta che l’uomo si sbaglia nel fare previsioni a lungo termine basandosi sui dati disponibili. Agli inizi del 1.800 la popolazione degli Stati Uniti era di meno di 10 milioni di individui, ma si andava accrescendo ad un ritmo impressionante tanto che il pastore anglicano Thomas Malthus, che aveva notato una forte sproporzione fra crescita della popolazione e crescita delle risorse alimentari, predisse per il futuro dell’umanità scenari apocalittici, nei quali l’uomo avrebbe sofferto la fame e sarebbe vissuto nella povertà.
Malthus aveva constatato che fra la fine del 1700 e gli inizi del 1800 la popolazione degli USA era cresciuta di circa il 3% all’anno, cioè ad un ritmo esponenziale o, come diceva lui, in progressione geometrica, mentre i mezzi di sussistenza crescevano, nella migliore delle ipotesi, in progressione aritmetica, cioè molto più lentamente. Ciò avrebbe portato ad una serie di conseguenze nefaste per l’umanità con il diffondersi fra la popolazione di quelli che lui chiamava vizi (guerre e infanticidi) e miserie (carestie ed epidemie). La differenza fra le due categorie di calamità sta nel fatto che le prime sono razionali e possono essere evitate mentre le seconde sono naturali e quindi sfuggono alle possibilità di controllo da parte dell’uomo. Le sciagure paventate da Malthus non si realizzarono: il popolo americano non soffrì la fame né visse nella miseria, ma soprattutto non continuò ad accrescersi al ritmo del 3% annuo. Se fossero state rispettate le previsioni di Malthus la popolazione degli Stati Uniti (affamata e povera) oggi sarebbe di quasi 2 miliardi di persone, mentre è di poco superiore ai 270 milioni e nessuno (o quasi) vive in miseria. Se sono difficili le previsioni sugli incrementi demografici, ancor più difficili sono quelle sui loro effetti.
Agli inizi degli anni 70 gli aderenti al Club di Roma, un gruppo di ricercatori che si occupava di questo problema, formularono la teoria della cosiddetta “crescita zero” secondo la quale, per salvare l’umanità, sarebbe stato necessario fermare la crescita sia della popolazione, sia dello sviluppo industriale che causava danni gravi e irreparabili all’ambiente come l’inquinamento e lo sfruttamento selvaggio delle risorse naturali. Anche in questo caso ci si era sbagliati. La popolazione da allora ad oggi aumentò quasi raddoppiando di numero e ancora di più aumentò la produzione industriale con la conseguenza di un sensibile miglioramento del tenore di vita degli abitanti del mondo industrializzato.
Ecco dove sta il vero problema legato allo sviluppo industriale e di conseguenza al tasso di crescita della popolazione: esso non è distribuito equamente fra tutti gli abitanti della Terra. Lo sviluppo industriale mondiale è in realtà prevalentemente circoscritto ai paesi già industrializzati in cui è relativamente basso il tasso di crescita della popolazione. Se il processo di sviluppo economico continuerà in futuro così come attualmente è strutturato, non c’è speranza che il divario fra paesi poveri e paesi ricchi possa ridursi: “Il ricco si farà sempre più ricco, mentre il povero farà figli”.
Oggi non si parla più di crescita zero ma di “sviluppo sostenibile” e, secondo il parere degli esperti del settore, la popolazione mondiale continuerà a crescere ancora per un certo tempo ma lo farà ad un ritmo sempre più lento fino a quando, raggiunto nella seconda metà del XXI secolo il livello di 11-12 miliardi di individui, comincerà a calare. Saranno giuste le previsioni? Lo sapremo fra cent’anni.
I LOGARITMI E LA CRESCITA DEI BATTERI
Il nome di logaritmo deriva dal greco dove “lògos” significa discorso, ragione e “arithmos” significa numero, quindi letteralmente il logaritmo sarebbe il “numero della ragione”: un nome altisonante, ma in realtà, come abbiamo visto, si tratta semplicemente di un esponente.
Abbiamo detto che i logaritmi trovano svariate applicazioni. Fra queste vi è pure quella di una comoda e chiara rappresentazione di alcuni diagrammi i quali sarebbero illeggibili, o quanto meno poco significativi, se non si facesse uso dei logaritmi. Vi sono infatti alcune grandezze che crescono così rapidamente, al variare di altre, che diventa impossibile rappresentarle efficacemente su un foglio mantenendo la scala reale dei valori.
Per chiarire il concetto facciamo l’esempio della crescita dei batteri. I batteri sono organismi viventi fra i più semplici e i più piccoli che si conoscano. Sono formati da una sola cellula della grandezza del millesimo di millimetro e il loro peso è dell’ordine del miliardesimo di milligrammo, ossia ce ne vorrebbero mille miliardi per fare un grammo. I batteri si riproducono con estrema rapidità per semplice scissione, cioè si dividono a metà e poi ciascun individuo si accresce e, raggiunta la dimensione adulta, subisce una nuova scissione. Ora, se le condizioni ambientali sono favorevoli, si possono avere anche tre generazioni in un’ora. Immaginiamo quindi di voler calcolare la crescita di una popolazione di batteri partendo da un singolo esemplare: dopo venti minuti ne avremmo già 2, dopo quaranta minuti 4 e dopo un’ora ossia dopo tre generazioni 8, dopo 2 ore, cioè dopo 6 generazioni 32 (26), dopo 5 ore 32.768 (215) e così via secondo le potenze del 2.
Il numero dei batteri aumenta secondo le potenze del 2 perché la cellula si divide in due ad ogni generazione, se la cellula si dividesse simultaneamente in tre il numero aumenterebbe secondo le potenze del 3 e se si dividesse in 10, secondo le potenze del 10. Il numero dei batteri che si riproduce per semplice scissione può essere quindi rappresentato attraverso la seguente funzione esponenziale:
y = 2x
in cui y è il numero dei batteri e x il numero delle generazioni.
Applicando l’equazione scritta sopra, è facile calcolare il numero teorico di batteri presenti dopo un certo numero di generazioni partendo da un singolo batterio. Per esempio si calcola che dopo 72 generazioni, cioè, nel nostro esempio, dopo un giorno, i batteri sarebbero diventati 272 che fa circa quattromila settecento miliardi di miliardi (4,7·1021), un numero di batteri che, nonostante il peso irrisorio di un singolo esemplare, corrisponde a un peso complessivo di 4.700 tonnellate. Ci vorrebbe un migliaio di camion caricati fino all’orlo per portarli via tutti. Naturalmente non si arriva mai a questi eccessi perché l’ambiente naturale non è illimitato e immutabile e quindi molto prima di avere una densità massima di circa un miliardo di individui per cm3 il numero tende a restare stazionario. Tuttavia, sperimentalmente, si possono realizzare le condizioni desiderate mettendo a disposizione dell’organismo un terreno di coltura molto ampio e stabile, nel quale può essere studiato il fenomeno dell’accrescimento teorico dei batteri o di altri esseri viventi.
A differenza di quanto succede fra gli uomini in cui, come abbiamo visto, il tasso di incremento demografico cresce con il crescere della popolazione, in tutti gli altri esseri viventi il tasso di incremento demografico tende a diminuire con l’ingrossarsi della popolazione. Questo dipende da una serie di fattori fra cui la scarsa disponibilità di alimenti dovuta al superaffollamento e la crescente concentrazione di prodotti di rifiuto derivati dal loro stesso metabolismo. In generale la curva di crescita di una popolazione sale velocemente all’inizio, ma poi si arresta. Questo tipo di curva, che prende il nome tecnico di “curva logistica”, è anche chiamata curva ad “S” per la sua forma. Ora, poiché questo modo di accrescersi di una popolazione vale per tutti i viventi non è pensabile che solo per l’uomo esso debba fare eccezione. Pertanto alla attuale fase di crescita esponenziale della popolazione umana seguirà inevitabilmente una fase stazionaria, se non addirittura di regressione. Quel che conta è vedere in che modo questa fase di arresto verrà raggiunta, perché le conseguenze saranno diverse a seconda che a fermare la crescita della popolazione umana sarà l’uomo stesso facendo uso dell’intelligenza di cui è dotato o la natura, la quale applicherà le leggi che essa sola conosce e che non sono certo leggi favorevoli all’uomo.
Se ora volessimo rappresentare con un’immagine geometrica la crescita dei batteri, dovremmo, come già sappiamo, tracciare su un foglio di carta due rette perpendicolari che si incontrano in un punto detto origine degli assi e quindi, scelte opportunamente le unità di misura, segnare su ciascuna retta una serie di punti che corrisponde a determinati valori delle grandezze in gioco. Ponendo, ad esempio, sull’asse orizzontale del piano i tempi e sull’asse verticale il numero dei batteri ci renderemmo subito conto che per quanto piccola fosse stata l’unità di misura scelta, già dopo una decina di generazioni il foglio di carta non sarebbe più sufficiente a contenere il diagramma.
A questo punto ci verrebbero tuttavia in soccorso i logaritmi. Se sull’asse delle ordinate (quello verticale) invece che segnare il numero delle cellule si riportasse il logaritmo di tale numero il diagramma diventerebbe più contenuto e di più facile lettura. In verità facendo ricorso ai logaritmi il disegno, oltre a cambiare dimensioni, cambierebbe anche forma divenendo una retta e quindi non rispecchierebbe più la realtà rappresentata da una curva a J. Tuttavia lo schema apparirebbe molto più chiaro e lo scopo che ci si era prefissati sarebbe stato raggiunto.
Partire da un singolo batterio per sapere quanti ve ne saranno dopo un certo tempo è un caso del tutto teorico. Normalmente quello che interessa sapere è quanti diventeranno i batteri (o qualsiasi altra cosa che si accresca in modo esponenziale), dopo un certo numero di generazioni, se si parte da un determinato numero iniziale. L’equazione utile per dare risposta a questo tipo di quesito è la seguente:
N = N0 · 2x
in cui N è il numero di batteri che sarà presente dopo un certo numero di generazioni, N0 è il numero iniziale di batteri e x è il numero delle generazioni che si vuole considerare. Si noti che per ottenere il numero dei batteri finali bisogna moltiplicare 2x per il numero iniziale di essi. La conseguenza di questa operazione è che il numero finale dei batteri dipende sensibilmente anche dal numero iniziale e non solo dal valore della x. La logica dell’accrescimento esponenziale, come abbiamo accennato all’inizio, è proprio questa: più si è e più si diventa.
Spesso non interessa tanto sapere quanti batteri (o più in generale quanti elementi di un insieme che si accresce) si avranno dopo un certo numero di generazioni, ma piuttosto quanti saranno diventati dopo un certo tempo (ad esempio dopo un giorno). In questo caso basta moltiplicare il numero delle generazioni (k), comprese nell’unità di tempo, per il tempo (t) di durata del processo e porre il prodotto di queste due grandezze ad esponente del numero che rappresenta i frammenti in cui si divide ogni singolo oggetto di partenza (due nel nostro esempio).
Sostituendo quindi k·t a x, l’equazione relativa ai batteri, scritta sopra, diventa:
N = N0 · 2k·t
In questo caso (base della potenza uguale a 2), il reciproco di k, cioè 1/k, rappresenta il tempo necessario per raddoppiare il numero degli elementi presenti. Se ad esempio fosse k = 3, cioè tre divisioni all’ora, come nell’esempio dei batteri proposto in precedenza, un terzo di ora (ossia venti minuti), sarebbe il tempo necessario affinché il numero degli elementi, presenti in un dato istante, raddoppiasse in seguito alle divisioni successive.
IL DECADIMENTO RADIOATTIVO E IL NUMERO e
Il decadimento radioattivo è un fenomeno che si presta molto bene ad essere analizzato attraverso i concetti che abbiamo esposto precedentemente. Le sostanze radioattive sono dei composti chimici costituiti di atomi che si decompongono spontaneamente in altri atomi non radioattivi. Il fenomeno del decadimento radioattivo è di tipo esponenziale e l’equazione che dà la misura secondo cui la massa di sostanza radioattiva diminuisce nel tempo è la seguente:
m = m0 · e–λ·t
dove m è la massa della sostanza radioattiva al tempo t, m0 è la massa della sostanza radioattiva che era presente all’inizio dell’esperimento, cioè al tempo t=0, e è un numero irrazionale che vale circa 2,7182 e rappresenta la base dei cosiddetti logaritmi naturali, e infine λ (lambda) è una costante detta “costante di decadimento radioattivo” il cui valore è un numero caratteristico di ciascuna sostanza radioattiva e dà la misura della maggiore o minore rapidità con cui avviene il processo di trasformazione. Più è grande il valore di lambda e maggiore è il numero degli atomi radioattivi che si trasformano in atomi non radioattivi nell’unità di tempo e quindi più rapido è il processo di decadimento. Come si vede si tratta di una formula molto simile a quella che è stata usata per definire la crescita dei batteri in condizioni ideali. La differenza più sostanziale sta nel segno negativo che compare davanti all’esponente di e. Esso suggerisce che la legge di decadimento radioattivo è una legge di tipo esponenziale decrescente, cioè una legge la quale mostra che con il passare del tempo gli elementi presenti all’inizio diminuiscono e non aumentano di numero, come avveniva invece nel caso dei batteri.
E’ opportuno, a questo punto, chiarire meglio il significato del numero e, detto numero di Eulero in onore di Leonhard Euler (latinizzato in Eulero), un matematico svizzero vissuto nel diciottesimo secolo, che lo presentò in un lavoro pubblicato nel 1748. Il numero e in realtà era già noto a Nepero e anzi fu proprio il matematico scozzese ad introdurlo per primo nei calcoli, anche se sotto altra forma: per questo motivo esso è chiamato anche numero di Nepero. Il numero e è un numero irrazionale trascendente: irrazionale perché non è esprimibile come rapporto fra due numeri interi e trascendente perché l’equazione che lo definisce trascende le normali operazioni di calcolo.
Qualsiasi numero intero e molti numeri decimali possono essere rappresentati sotto forma di frazione: 5 ad esempio può essere scritto 5/1 o 10/2 e così via; 0,5 può essere scritto 1/2 o 5/10 o in molti altri modi, ma sempre come rapporto di numeri interi. Vi sono tuttavia dei numeri che non possono essere rappresentati sotto forma di frazione di numeri interi: ad esempio, la radice quadrata di 2 il cui valore è 1,4142135… e via avanti verso un numero infinito di decimali apparentemente disordinati, non può essere rappresentata sotto forma di rapporto di numeri interi. Anche π, che esprime il rapporto fra la circonferenza e il suo diametro, è un numero che non può essere espresso come rapporto di due numeri interi, e quindi è anch’esso un numero irrazionale. Altro numero irrazionale è il numero e il cui valore, 2,718281…, è dato dal limite cui tende l’espressione (1 + 1/n)n quando n tende all’infinito. Il numero e, insieme a π, è il numero irrazionale più importante che esista in matematica, ma mentre π ha un riscontro geometrico nella realtà e non rappresenta nulla di concreto. Pi greco ed e oltre ad essere numeri irrazionali sono anche trascendenti perché i calcoli che portano alla loro definizione trascendono, ossia vanno oltre le normali operazioni algebriche. Il numero radice di 2, ad esempio, è un numero irrazionale ma non trascendente perché è la soluzione di un’equazione algebrica (x2 = 2) cioè di un’espressione che contiene un numero finito di termini, mentre per arrivare ad e bisogna risolvere espressioni che contengono un numero infinito di termini. Può sembrare strano che un numero così particolare come e sia tanto diffuso nei campi più disparati delle scienze naturali, ma bisogna considerare che molti problemi di matematica applicata trovano una rappresentazione più chiara e significativa proprio quando vengono espressi in termini di potenze di e.
Per comprendere il significato del numero e riprendiamo l’esempio del milione di lire depositato in banca all’interesse del 7% annuo. Come si ricorderà, dopo un anno il milione iniziale diventava un milione e 70 mila lire, dopo due anni 1 milione e 145 mila lire circa, dopo tre anni 1.225.000 lire circa e così via verso somme sempre più alte, finché il valore nel giro di circa 10 anni risulta raddoppiato. L’interesse computato su questa base è chiamato interesse composto ed è più redditizio di quello semplice che invece è calcolato sul solo capitale iniziale e non è fruttifero nei successivi periodi.
Si noti che durante tutto il primo anno il milione di capitale depositato in banca è rimasto un milione e l’interesse è scattato solo all’inizio del secondo anno; anche il milione e 70 mila lire si mantiene uguale a sé stesso per tutto il secondo anno e solo alla fine di questo avviene la capitalizzazione. Cosa sarebbe successo se l’interesse del 7% invece che aggiungersi alla fine di ogni anno si fosse distribuito lungo tutto il suo corso procedendo alla capitalizzazione con maggior frequenza, ad esempio ogni tre mesi o addirittura ogni settimana? Il guadagno sarebbe stato maggiore?
Se la capitalizzazione venisse fatta ogni settimana, il milione di partenza crescerebbe al ritmo dello 0,1346% circa alla settimana, cioè dopo la prima settimana già sarebbe diventato 1.001.346 lire e su questa cifra verrebbe calcolato l’interesse da aggiungere allo scadere della seconda settimana. Ebbene, è facile dimostrare che calcolando l’interesse tutte le settimane, invece che aspettare fine anno, il capitale iniziale dopo 10 anni invece che raddoppiare diventerebbe di quasi 2 milioni e 700 mila lire. Se la capitalizzazione venisse fatta ancora più di frequente, ad esempio, ogni giorno o ogni ora, il capitale, dopo 10 anni, si avvicinerebbe molto alla cifra di 2.718.281 lire. Questo tipo di capitalizzazione si chiama capitalizzazione continua e conduce alla definizione del numero e.
Il capitale complessivo aumenta di valore quanto più di frequente avviene la capitalizzazione e può essere calcolato risolvendo la seguente espressione matematica: (1 + 1/n)n dove n rappresenta la frequenza della capitalizzazione. E’ facile verificare che più aumenta il valore di n, cioè più frequente è la capitalizzazione, e più l’espressione si avvicina al valore di 2,718281828459… Per n uguale a 1, l’espressione diventa (1 + 1/1)1 = 2, che sta a significare che il capitale di partenza raddoppia. Per n = 365 (i giorni dell’anno) l’espressione diventa (1 + 1/365)365 = 2,714567… Se ad n si assegna un valore ancora più grande, ad esempio 8.760, il numero delle ore presenti in un anno, l’espressione diventa: (1 + 1/8760)8760 = 2,7181266…
Ma l’espressione (1 + 1/n)n, come abbiamo detto, definisce il numero e quando n tende all’infinito. E’ facile dimostrare che il capitale complessivo, quello che con termine tecnico si chiama il montante (M), di un certo capitale iniziale (P), investito ad un determinato tasso di interesse (), alla fine di un certo numero di anni (t), qualora questo interesse venisse capitalizzato continuamente, può essere calcolato utilizzando la formula seguente:
M = P·e∙t
Il capitale di un milione, investito all’interesse del 7% annuo, a capitalizzazione continua, dopo un anno diventa 1.072.506 lire anziché 1.070.000, come sarebbe stato a capitalizzazione annuale.
LA “VITA” DEGLI ATOMI RADIOATTIVI
I logaritmi possono avere una base qualsiasi, purché sia un numero positivo diverso da 1, ma i logaritmi più comuni sono quelli in base 10 e in base e. I logaritmi in base 10 si chiamano anche decimali (o volgari, o di Briggs dal nome del matematico inglese che per primo ne suggerì l’uso) e si indicano con il simbolo Log (con la L maiuscola per motivi grafici), invece che log10. I logaritmi in base e si chiamano invece naturali (o iperbolici, o neperiani), e si indicano con il simbolo ℓn, invece che loge.
Torniamo ora alle sostanze radioattive ed esaminiamo il comportamento di un milione di atomi di una di queste sostanze che si disintegra al ritmo di un atomo su mille all’ora. Dopo un’ora, del milione di atomi di partenza, se ne saranno disintegrati mille e, se tale numero rimanesse costante, dopo mille ore se ne sarebbero disintegrati un milione, cioè tutti. Però nel caso del decadimento radioattivo le cose non vanno in questo modo, perché ciò che rimane costante non è il numero (1.000 atomi), ma l’intensità del fenomeno, cioè l’1 per mille all’ora (un atomo che si disintegra ogni ora su mille che sopravvivono). Il decadimento radioattivo infatti non è un fenomeno di tipo lineare ma esponenziale e pertanto, dopo 1.000 ore, gli atomi rimasti, del milione di partenza, non saranno zero ma 367.879, cioè un numero che si ricava dal rapporto di 1 su e, che fa 0,367879…, moltiplicato per un milione.
L’equazione che esprime la legge del decadimento radioattivo può essere formulata in termini logaritmici, e poiché in questa legge compare il numero e, si devono usare i logaritmi naturali:
ℓn m = ℓn (m0 ∙ e –λ·t)
Ora, siccome il logaritmo di un prodotto è uguale alla somma dei logaritmi dei singoli fattori e il logaritmo di una potenza è uguale al prodotto dell’esponente per il logaritmo della base della potenza, l’espressione scritta sopra può essere riformulata nel modo seguente:
ℓn m = ℓn m0 – λ · t ·ℓn e
Quindi, tenendo conto che il logaritmo di base e di e vale 1 (come d’altra parte vale 1 qualsiasi logaritmo della propria base), l’equazione può essere anche scritta in quest’altro modo:
ℓn m0 – ℓn m = λ · t
Scritta sotto questa forma, l’equazione mostra che la differenza fra i logaritmi di una certa massa di sostanza radioattiva è sempre la stessa in intervalli di tempo uguali (λ è una costante). In altri termini si può anche dire che se si considera un determinato intervallo di tempo, per esempio un’ora, la differenza fra il logaritmo del numero degli atomi radioattivi presenti alla fine dell’ora e quello degli atomi presenti all’inizio dell’ora è sempre la stessa, indipendentemente dal momento in cui viene scelto l’intervallo di tempo di un’ora, cioè subito, fra un giorno o fra una settimana.
Ora, poiché la differenza fra i logaritmi di due numeri è uguale al logaritmo del loro quoziente, se è costante la differenza fra i logaritmi delle masse delle sostanze radioattive, deve essere costante anche il logaritmo del loro quoziente, ma se è costante ℓn (m0/m), è costante pure il rapporto m0/m.
Più in generale possiamo quindi affermare che in una crescita (o in una decrescita) di tipo esponenziale il quoziente fra il numero di individui all’inizio e quello alla fine di un determinato intervallo di tempo si mantiene costante e, siccome una successione di numeri nella quale è costante il quoziente fra ciascun termine e il suo precedente è una progressione geometrica, possiamo confermare che i valori di una funzione esponenziale costituiscono una progressione geometrica.
Da come viene espresso un incremento (o un decremento) siamo in grado quindi di capire immediatamente se esso è di tipo esponenziale oppure no: quando un incremento (o un decremento) viene espresso con un numero esso è di tipo lineare, se invece viene espresso in termini percentuali esso è sicuramente di tipo esponenziale.
Come abbiamo già visto in precedenza, anche nel caso del decadimento radioattivo, il reciproco di lambda rappresenta una misura di tempo e precisamente esso esprime quello che in fisica nucleare si chiama la “vita media” di un elemento radioattivo. Non tutti gli atomi radioattivi di una certa specie (per esempio Uranio) si trasformano nello stesso tempo: ve ne sono alcuni che lo fanno immediatamente altri che lo fanno dopo tempi più lunghi. E’ un po’ quello che avviene per gli uomini: alcuni hanno vita breve ed altri sono molto longevi. Per l’uomo la vita media si calcola sommando la durata della vita di un certo numero di persone e poi dividendo questo valore per il numero di persone considerate. Analogamente, per le sostanze radioattive, questo numero si ottiene sommando i tempi di vita effettiva dei singoli atomi e poi dividendo questa somma per il numero totale degli atomi considerati. Il calcolo è piuttosto complesso, ma il risultato a cui si perviene è molto semplice: la vita media di un elemento radioattivo è misurata proprio dal reciproco di λ.
Normalmente, però, in fisica nucleare, per indicare il tempo di “vita” di una sostanza radioattiva non si fa uso della grandezza espressa sopra, ma del cosiddetto “periodo di semitrasformazione” o “tempo di dimezzamento”. Esso rappresenta il tempo necessario alla disintegrazione della metà di una determinata massa di sostanza radioattiva. Per calcolare questo valore basta porre, nell’equazione logaritmica scritta in precedenza, N0/2 (metà della sostanza di partenza) al posto di N. Risulta quindi:
ℓn [N0/(N0/2)] = t½ · λ
da cui:
t½ = ℓn 2/λ = 0,693/λ .
Come si può vedere il “periodo di semitrasformazione”(t½) di una sostanza radioattiva è circa i 7/10 di 1/λ, quindi è leggermente inferiore a quella che abbiamo chiamato la “vita media” di una sostanza radioattiva.
I logaritmi di numeri negativi non esistono, esistono però logaritmi di numeri positivi maggiori di 1 e logaritmi di numeri positivi minori di 1. I primi danno come risultato valori positivi, i secondi valori negativi: ad esempio, il logaritmo in base 10 di 1000 è 3 e il logaritmo in base 10 di 1/1000 è -3.
LA CLASSIFICAZIONE DELLE ROCCE CLASTICHE
Anche i petrografi, ovvero i geologi che studiano i materiali rocciosi che compongono la crosta terrestre, utilizzano i logaritmi per classificare un tipo particolare di rocce. Si tratta delle cosiddette rocce detritiche o clastiche (dal greco clao = spezzo), cioè di quelle rocce che si sono formate per accumulo di frammenti di rocce preesistenti. La classificazione di queste rocce è basata fondamentalmente sulle dimensioni e sulla forma dei frammenti che le costituiscono. Le taglie di questi frammenti vengono ripartite in numerosi gruppi che sono detti classi granulometriche. Ogni classe granulometrica raggruppa in sé i frammenti di roccia le cui dimensioni sono comprese fra due valori limite scelti arbitrariamente, ma posti all’interno di una determinata scala di grandezze detta “scala di Wentworth”. Le dimensioni limite delle classi granulometriche sono rappresentate dalle potenze intere positive e negative del 2. Quindi, in millimetri, esibiscono i seguenti valori: …256, 128, 64, 32, 16, 8, 4, 2, 1, 1/2, 1/4, 1/8, 1/16, 1/32, 1/64, 1/128, 1/256… Questi numeri sono le potenze del 2 elevato rispettivamente agli esponenti: …8, 7, 6, 5, 4, 3, 2, 1, 0, -1, -2, -3, -4, -5, -6, -7, -8 …, che ne rappresentano quindi i logaritmi di base 2.
Le classi granulometriche sono molte, ma i limiti dimensionali più importanti sono solo due: 2 mm e 1/16 mm. Le rocce con granuli di diametro compreso entro questi due estremi sono dette, con termine derivato dal latino, areniti o psammiti (dal greco psammos = sabbia). Quelle formate di frammenti di dimensioni superiori a 2 mm sono dette ruditi o psefiti (dal greco psephos = ciottolo) e infine quelle con taglia inferiore a 1/16 mm sono dette lutiti o peliti (dal greco pelos = argilla). All’interno di ciascuna classe principale si può procedere ad un’ulteriore classificazione più dettagliata. Le rocce clastiche si dividono inoltre in due grandi gruppi a seconda che i frammenti di cui sono costituite siano sciolti oppure cementati insieme.
Si parte, in pratica, da massi con diametro superiore a 256 mm per giungere a particelle con diametro inferiore a 1/256 mm. Le rocce psefitiche sono quelle in cui i clasti hanno dimensioni superiori a 2 mm di diametro e comprendono le ghiaie che sono depositi di detriti piuttosto grossolani a spigoli arrotondati in conseguenza del trasporto da parte di corsi d’acqua. Se gli spigoli dei frammenti sono vivi si parla di detriti di falda o brecce di pendio. Quando i frammenti sono fra loro cementati le rocce prendono il nome di puddinghe (con ciottoli arrotondati) e brecce (con ciottoli a spigoli vivi).
Le rocce psammitiche hanno i clasti del diametro compreso fra 2 mm e 1/16 mm e prendono il nome di sabbie o arene se i granuli sono liberi e arenarie se i granuli sono cementati. Le arenarie sono molto usate come materiale da costruzione. Fra esse assai note sono quelle toscane utilizzate per la edificazione dei centri storici delle principali città della regione, compresa Firenze, in cui ad esempio il “macigno”, un’arenaria a grana media e cemento calcareo, è servito per la costruzione del basamento di palazzo Strozzi e la “pietra serena” una varietà di colore grigio azzurrognolo forma lo scalone della Galleria degli Uffizi.
Infine le rocce pelitiche hanno i clasti del diametro che va da 1/16 di millimetro (0,0625 mm) fino a valori inferiori a 1/256 di millimetro (0,0039 mm). Quando la grana è compresa fra 1/16 di mm e 1/128 di mm si hanno le siltiti, cosiddette perché composte da un sedimento chiamato silt (parola inglese che significa fango). Quando le dimensioni dei grani sono ancora inferiori a questi valori, si hanno le argilliti. Siltiti e argilliti vengono anche dette, con termine comprensivo, limi e si formano per processi di trasporto e di deposito fluviale (limi fluviali), per trasporto e deposito ad opera del vento (loess o limi eolici) e per trasporto e deposito glaciale (lehm o limo glaciale). Le argille sono caratterizzate da forte igroscopicità, ossia hanno la tendenza a trattenere l’acqua. Quando piove il terreno argilloso tende ad aumentare di volume, mentre in periodi di siccità, a causa dell’evaporazione dell’acqua, la massa argillosa diminuisce di volume e su di essa appaiono profonde spaccature.
Abbiamo già visto che i logaritmi si dimostrano utili quando si deve far uso di diagrammi; nel caso di sedimenti clastici l’uso dei logaritmi nella costruzione di diagrammi è ancora più evidente, perché serve a rappresentare in modo facilmente comprensibile la composizione granulometrica di tali sedimenti. Attraverso i diagrammi risulta pertanto comodo analizzare le caratteristiche granulometriche del sedimento e quindi risalire all’ambiente di formazione e alla natura dei clasti. Si riportano allora, sull’asse delle ascisse, i valori limite delle classi granulometriche dei clasti esaminati e sull’asse delle ordinate le quantità, espresse ad esempio in percentuale, del peso del sedimento delle varie classi. Quello che si ottiene in questo caso è un grafico discontinuo a gradini, detto istogramma.
Se l’asse delle ascisse viene suddiviso in segmenti proporzionali ai logaritmi dei valori limite che individuano le classi granulometriche, invece che ai valori stessi, si ottiene il risultato di mantenere equidistanti i valori numerici fra le classi granulometriche successive e nel diagramma compare una serie di rettangoli le cui basi sono tutte uguali e le cui altezze proporzionali alla quantità dei clasti compresi nella classe granulometrica considerata. Se venissero invece posti, sull’asse delle ascisse, i valori reali dei clasti, si otterrebbero rettangoli con le basi di dimensioni diverse e l’analisi del diagramma non sarebbe più così agevole e immediata.
LE MAGNITUDINI STELLARI
Non vi è campo delle scienze naturali in cui non si faccia uso dei logaritmi per descrivere qualche fenomeno relativo a quello specifico settore di studio. In astronomia, ad esempio, lo splendore delle stelle viene valutato in termini logaritmici attraverso le cosiddette “classi di grandezza” o, con termine moderno, “magnitudini”.
Dagli antichi Greci abbiamo mutuato il criterio di suddividere le stelle in classi di grandezze. Due secoli prima di Cristo Ipparco di Nicea, uno dei più grandi astronomi dell’antichità, suddivise le stelle a seconda del grado di luminosità in sei classi di grandezza, ponendo nella prima le più fulgide, cioè quelle che la sera appaiono in cielo per prime, un po’ dopo il tramonto del Sole; nella seconda classe, quelle che si rendono visibili quando il cielo è un po’ più scuro e quindi, nelle classi successive, quelle con luce via via più fioca. Nella sesta classe infine vennero collocate le stelle appena visibili nelle migliori condizioni fisiche, cioè quando è notte fonda con il cielo perfettamente sereno e senza luna.
Gli antichi naturalmente classificarono le stelle ad occhio nudo, quindi senza far ricorso a strumenti ottici che non erano ancora stati inventati. Essi però posero molta cura nel fare sì che l’occhio, trasferendosi da una classe all’altra, valutasse in modo sempre uguale la differenza di splendore. Per esempio, una stella di prima grandezza doveva apparire più brillante di una di seconda grandezza quanto quest’ultima lo era di una di terza e così via per le altre. E’ opportuno far notare che la scala delle grandezze stellari adottata dagli antichi è rovesciata, nel senso che le stelle di maggiore luminosità hanno magnitudine minore (una stella di prima grandezza è più brillante di una stella di seconda grandezza).
Verso la metà del diciannovesimo secolo, quando furono disponibili strumenti tecnici adeguati e metodi di misurazione raffinati, si avvertì l’esigenza di misurare con maggiore precisione e accuratezza l’intensità della luce che proviene dalle stelle. Potendo quindi disporre di dati molto precisi si procedette al perfezionamento della classificazione proposta dai Greci togliendo anche quel tanto di arbitrario e di soggettivo che era implicito nella loro formulazione. Da quel momento si preferì anche usare il termine di “magnitudine” al posto di “grandezza” al fine di evitare di collegare erroneamente lo splendore alle dimensioni di una stella. Al riguardo forse è opportuno precisare che le stelle sono troppo lontane perché si possano valutare, al telescopio, le loro dimensioni reali.
In realtà gli antichi parlavano di grandezza delle stelle riferendosi alla loro luminosità perché in effetti le stelle più brillanti ci appaiono anche più grandi. La stessa cosa accade quando osserviamo una qualsiasi fotografia del cielo stellato: le immagini delle stelle presentano dimensioni differenti. Il fenomeno è dovuto alla conformazione della parte sensibile dell’occhio dove gli elementi che costituiscono la retina (coni e bastoncelli) quando vengono colpiti dalla luce irradiano essi stessi verso gli elementi circostanti in misura tanto maggiore quanto più è intensa la luce incidente. La stessa cosa avviene sulla lastra fotografica sulla quale gli elementi sensibili sono costituiti da granuli di bromuro di argento.
Torniamo ora alla scala di grandezza delle stelle e al suo aggiornamento. Quale correlazione fisica – ci si chiese – intercorre fra il flusso di luce che proviene da una stella e la sensazione recepita dai nostri occhi? Un giovane assistente del Radcliffe Observatory di Oxford, Norman Robert Pogson, intorno alla metà dell’Ottocento, intuì che la strada giusta per affrontare il problema era quella indicata dalla legge psicofisica di Fechner e Weber la quale stabilisce che la intensità di una sensazione avvertita coscientemente è proporzionale al logaritmo dell’intensità dello stimolo che la produce, quindi è meno intensa di esso. Se la risposta che i nostri organi di senso danno agli stimoli fosse direttamente proporzionale alla loro intensità rischieremmo di finire in breve tempo con occhi, orecchie e gli altri organi di senso fuori uso. Essi sono invece in grado di ridurre l’intensità degli stimoli secondo il loro logaritmo quindi, mentre l’intensità dello stimolo cresce in progressione geometrica, quella della sensazione cresce solo in progressione aritmetica. Utilizzando le proprietà delle progressioni potremmo anche dire che ad uguali differenze di sensazioni corrispondono uguali rapporti di intensità degli stimoli. Se non avessimo questa capacità selettiva nei confronti degli stimoli che colpiscono i nostri organi di senso rimarremmo accecati dalla luce di una folgore e assordati dal suono di una sirena. Una lastra fotografica colpita da luce troppo intensa rimane “bruciata” e un apparecchio acustico, a differenza dell’orecchio umano, come ben sanno coloro che lo usano, non è in grado di selezionare l’intensità dei suoni che raccoglie.
La legge di Fechner e Weber, applicata al caso delle stelle, assume la forma seguente:
m = k · Log J
dove m (magnitudine) è l’immagine di una stella che si forma nel nostro occhio e rappresenta quindi la sensazione, mentre J è la quantità di energia luminosa che incide sul recettore, cioè è lo stimolo; k è una costante di proporzionalità il cui valore e significato verrà chiarito in seguito. Log è il simbolo del logaritmo decimale.
Pogson osservò che il rapporto fra la quantità di luce emessa da due stelle che differivano di una classe di luminosità (secondo la valutazione di Ipparco) era di circa due volte e mezzo, cioè, in pratica, l’energia luminosa emessa ad esempio da una stella di prima grandezza era di circa due volte e mezza superiore a quella emessa da una stella di seconda grandezza (teniamo sempre presente che la scala delle grandezze è rovesciata). Ora, poiché il valore di 2,5 individuato empiricamente da Ipparco è molto vicino a 2,512 che è la radice quinta di 100, Pogson scelse proprio questo valore come “ragione” della progressione geometrica che avrebbe dovuto individuare i valori di luminosità relativi alle nuove classi di magnitudine stellare.
In una progressione geometrica, come si ricorderà, il rapporto fra ciascun termine e il suo precedente è un numero fisso che rappresenta quello che viene chiamato la ragione della progressione: ebbene in questo caso si tratta di scrivere una progressione geometrica di ragione 2,512. Quindi, se assegniamo il valore 1 all’intensità della luce che proviene dalle stelle molto deboli che stanno al sesto posto della scala delle magnitudini, le stelle che occupano il 5° posto producono energia 2,512 volte maggiore, e così di seguito, sempre moltiplicando il valore precedente per 2,512, nei riguardi delle stelle di magnitudine maggiore. L’intensità della luce emessa dalle stelle che occupano dal 6° al 1° posto della scala è la seguente: 2,5120 2,5121 2,5122 2,5123 2.5124 2,5125 che corrispondono ai valori 1, 2,512, 6,310, 15,851, 39,818, 100,0 per le stelle rispettivamente di magnitudine 6, 5, 4, 3, 2 e 1.
Pertanto, secondo la proposta di Pogson, la luce di una stella di seconda magnitudine doveva essere 2,512 volte più debole della luce di una stella di prima magnitudine; la luce di una stella di terza magnitudine doveva essere 2,512 volte più debole della luce di una stella di seconda magnitudine e 6,31 (=2,512²) volte più debole di una di prima, e così via. Alla fine, una stella di sesta magnitudine doveva essere 100 volte meno luminosa di una di prima.
L’antica classificazione assume ora un aspetto più rigoroso che può essere anche espresso attraverso la seguente formula:
m1 – m2 = k · Log (J1/J2)
dove con m1 – m2 è indicata la differenza di magnitudine di due stelle le cui intensità luminose siano rispettivamente J1 e J2. Questa formula ci consente, qualora siano noti i valori delle intensità luminose di due stelle qualsiasi, di definire il valore di k. Se misuriamo, ad esempio, fra due stelle un rapporto di luminosità uguale a 100, sappiamo che si tratta di due stelle che stanno, all’interno della scala delle magnitudini, su posizioni distanti cinque gradini (ad esempio una al sesto e l’altra al primo posto): la differenza fra le magnitudini di queste due stelle (m1 – m2) è quindi uguale a 5, il valore della costante k risulta allora immediatamente definito. Infatti si ha:
5 = k · Log 1/100
da cui:
5 5
k = —————— = —— = – 2,5
Log1/100 – 2
Si faccia attenzione a non confondere questo 2,5 con il rapporto 2,512 che definisce la scala delle magnitudini.
Essendo noto il valore di k, la formula di Pogson assume ora il seguente aspetto:
m1 – m2 = – 2,5 · Log (J1/J2)
Il segno negativo indica semplicemente che alle stelle più deboli viene attribuito il valore di magnitudine più alto e a quelle più luminose il valore più basso, come abbiamo più volte ricordato.
La formula di Pogson, attraverso la misura esatta dei flussi luminosi delle singole stelle, consente di andare al di là delle sei classi di grandezza considerate dagli antichi e definire anche magnitudini di valori non interi. Con l’uso dei telescopi più potenti oggi è possibile fotografare stelle fino alla 24ª magnitudine, e con i telescopi spaziali si può giungere fino alla 29ª magnitudine, cioè è possibile vedere oggetti luminosi che inviano meno luce, agli apparecchi riceventi, di quanta ne invierebbe una candela accesa sull’altra sponda dell’Oceano Atlantico.
Inoltre, sempre con la formula di Pogson, è possibile attribuire alle stelle più brillanti, che gli antichi classificavano indiscriminatamente di 1ª grandezza, magnitudini prossime a zero e anche negative. Così a Sirio, la stella più brillante del firmamento, oggi viene attribuita magnitudine -1,46 e a Vega 0,04. La scala vale ovviamente per qualsiasi corpo che brilli in cielo, e quindi non solo per le stelle. Venere, ad esempio, al momento del suo massimo splendore, ha magnitudine -4,4; la Luna piena è un astro di magnitudine -12,7 e il Sole ha magnitudine -26,7.
LE STELLE PIU’ LUMINOSE DEL FIRMAMENTO
Qualora sia noto il rapporto fra l’intensità della luce che proviene da due astri, applicando la legge di Pogson, è possibile ricavare la differenza di magnitudine dei due astri in oggetto. Se ad esempio una determinata stella apparisse 70 volte più luminosa di un’altra, la loro differenza di magnitudine si ricaverebbe immediatamente moltiplicando per 2,5 il logaritmo di 70 e poi cambiando segno al risultato. Eseguite le operazioni si otterrebbe –4,61 che è la differenza di magnitudine fra le due stelle prese in esame. Questo valore tuttavia non ci dice a quale classe di magnitudine appartengono le due stelle, ma semplicemente che quella meno luminosa ha una magnitudine 4,61 volte maggiore dell’altra. Se la prima fosse ad esempio di magnitudine 2,21 la seconda sarebbe di magnitudine 6,82 (non visibile ad occhio nudo).
Per fissare le classi di magnitudine delle singole stelle era necessario stabilire un “punto zero”, scegliere cioè una stella campione a cui riferire tutte le altre. Al fine di mantenere il miglior accordo possibile coi dati di luminosità dell’astronomia antica, il punto zero fu fissato attribuendo alla Stella Polare (che gli antichi classificavano di 2ª grandezza) un valore di magnitudine di 2,12. Questo valore tanto preciso fu scelto in seguito alla scoperta di una debole variabilità della stella. Ora, ad una stella che presentasse un flusso luminoso x volte inferiore o superiore a quello della Stella Polare verrebbe attribuita la magnitudine seguente: m = 2,12 ± 2,5 · Log x.
La formula di Pogson permette anche di conoscere il valore del rapporto fra le intensità luminose che provengono da due astri, se si conosce la differenza di magnitudine. Ad esempio Rigel, la stella più luminosa della costellazione di Orione, ha magnitudine 0,34 mentre Venere, al massimo dello splendore, ha magnitudo -4,4. Ebbene, sottraendo dalla magnitudine di Rigel quella di Venere si ottiene 4,74 che rappresenta la differenza di magnitudine fra i due astri. Dividendo questo valore per 2,5 si ottiene 1,9 che è il logaritmo di base 10 del rapporto fra le intensità luminose dei due corpi celesti. Quindi, elevando il 10 a 1,9 si ottiene 79,43, un numero che definisce di quanto è maggiore l’intensità luminosa dell’astro più splendente rispetto all’altro. Da Venere, quando è al massimo splendore, ci arriva quasi 80 volte più luce che da Rigel che è, essa stessa, una stella già molto luminosa. Si noti che, per i motivi che abbiamo espresso sopra, non si ha la sensazione di una così grande differenza di luminosità fra i due astri.
Per avere un’idea di quanto deboli appaiano le stelle di magnitudine al limite della sensibilità degli strumenti di rilevamento, basta ricordare che una stella di prima magnitudine è 100 volte più luminosa di una di sesta e questa è a sua volta 100 volte più splendente di una di 11ª magnitudine la quale è ancora 100 volte più luminosa di una stella di 16ª magnitudine e così via. In questo modo, scalando di cinque in cinque, si arriva facilmente a calcolare che una stella di 1ª magnitudine è un miliardo di volte più brillante di una di 26ª magnitudine. Se poi si volesse prendere in considerazione il Sole che ha una magnitudine di -26,7, l’intervallo di magnitudini astronomiche fra l’astro più brillante, che si vede in cielo, e quello meno brillante, che gli apparecchi riescono a segnalare, è di oltre 56 ordini di magnitudine corrispondenti ad un rapporto fra i flussi luminosi di 1022. Ciò significa che l’energia solare è decine di migliaia di miliardi di miliardi di volte superiore a quella che ci proviene dalle stelle più deboli.
Dai dati che abbiamo appena fornito emerge chiaro il motivo per il quale risulta più conveniente e più comodo usare la scala logaritmica (cioè le magnitudini) al posto della misura diretta degli splendori stellari. La ragione sta nel fatto che con i logaritmi si fa uso di quantità che impiegano un intervallo numerico molto limitato, rispetto ai valori di luminosità che sono invece molto grandi. Dire che due stelle differiscono di dieci classi di magnitudine è molto più comprensibile e immediato piuttosto che affermare che il rapporto fra i flussi luminosi dei due astri è diecimila.
Il numero delle stelle aumenta progressivamente con l’aumento della magnitudine. Vi sono solo tre stelle con magnitudine negativa: Sirio (-1,4), Canopo (-0,7) e Alpha Centauri (-0,27), mentre sette o otto hanno magnitudine intorno a zero. Sono circa 20 le stelle di 1ª magnitudine, circa 60 quelle di 2ª, circa 170 di 3ª, 400 di 4ª, 1000 di 5ª, 4000 di 6ª magnitudine e così via fino alla decima magnitudine, oltre la quale il numero delle stelle cresce vertiginosamente.
LA MAGNITUDINE ASSOLUTA DELLE STELLE
Le magnitudini che si ricavano dalla formula di Pogson sono apparenti in quanto ci danno un’indicazione del flusso luminoso che proviene dalle stelle indipendentemente dal fatto che queste stelle siano vicine o lontane e intrinsecamente molto o poco luminose. La magnitudine di una stella, come è stata definita in precedenza, oltre che dalla sua luminosità intrinseca, cioè dall’energia luminosa che realmente emette, dipende infatti anche dalla sua distanza. Due stelle che appaiono ugualmente brillanti potrebbero avere splendore intrinseco molto diverso e apparire uguali per luminosità solo per il fatto di essere poste a distanze diverse l’una dall’altra; viceversa due stelle che appaiono di luminosità diversa potrebbero avere in realtà splendore intrinseco identico, ma apparire di diversa magnitudine apparente solo per il fatto che non si trovano alla stessa distanza. E’ chiaro che l’interesse prevalente dell’astronomo è quello di conoscere il reale splendore di una stella perché da esso dipende l’energia che la stella effettivamente emette. A questa energia, a sua volta, è legata l’età della stella e lo stato attuale della sua evoluzione. Alla definizione di questa grandezza si arriva attraverso quella che viene chiamata la magnitudine assoluta (M).
Per magnitudine assoluta di una stella si intende la magnitudine apparente che essa avrebbe se fosse posta alla distanza, scelta in modo del tutto arbitrario, di 10 parsec (32,6 anni luce circa). Conoscendo la magnitudine apparente e la distanza di una stella è possibile calcolare quale luminosità avrebbe quella stessa stella se venisse posta a 10 parsec di distanza. Infatti la fisica insegna che la luminosità di un corpo diminuisce in modo proporzionale al quadrato della distanza: la luminosità di una stella posta a distanza doppia si riduce a 1/4, posta a distanza tripla si riduce a 1/9, e così via.
Con questa premessa, ed usando la formula di Pogson, è possibile ricavare una fondamentale relazione che lega tra loro la magnitudine assoluta M di una stella, la sua magnitudine apparente m e la distanza d espressa in parsec. Si procede nel modo che segue.
Siano Jd e J10 i flussi luminosi di due stelle poste rispettivamente alle distanze di d parsec e di 10 parsec. Siano m e M le rispettive magnitudini. Poiché, come abbiamo appena visto, il flusso luminoso di una stella diminuisce con l’inverso del quadrato della distanza, possiamo scrivere:
Jd /J10 = (10/d)2.
Ora, prendendo i logaritmi decimali di entrambi i membri dell’equazione e moltiplicando per 2,5 si ha:
2,5·Log Jd/J10 = 2,5·Log (10/d)²
da cui:
2,5·Log Jd/J10 = 2,5 · 2·(Log 10 – Log d)
quindi, poiché sappiamo che il logaritmo di base 10 di 10 vale 1, possiamo scrivere:
2,5·Log Jd/J10 = 5 · (1 – Log d)
e pertanto:
2,5·Log Jd/J10 = 5 – 5·Log d
Infine, ricordando la formula di Pogson, che in questo caso va scritta nel modo seguente:
M – m = 2,5 · Log Jd/J10
sostituendo i valori, avremo:
M – m = 5 – 5·Log d
da cui:
M = m + 5 – 5·Log d
L’applicazione di questa formula è molto semplice. Prendiamo ad esempio il Sole la cui luminosità apparente è -26,7 e di cui è nota la distanza: 150 milioni di kilometri, corrispondenti a 4,85·10-6parsec. Attraverso la formula riportata sopra, si ricava il valore della sua magnitudine assoluta nel modo seguente:
M = – 26,7 + 5 – 5·Log 4,85·10-6
da cui:
M = – 21,7 – 5·(- 5,31)
e quindi:
M = – 21,74 + 26,57 = + 4,83.
Se ipotizzassimo il nostro Sole alla distanza di 10 parsec (32,6 anni luce, quindi a circa 300.000 miliardi di kilometri invece che a soli 150 milioni dove effettivamente si trova), esso ci apparirebbe solo un poco più luminoso di una stella appena visibile ad occhio nudo. Non solo il Sole, ma anche il cielo cambierebbe radicalmente di splendore se venissero poste a 10 parsec tutte le stelle comprese fra la prima e la sesta magnitudine apparente. Queste si disporrebbero allora più o meno secondo una gerarchia determinata dalle loro masse in quanto la luminosità intrinseca di una stella è direttamente proporzionale alla quantità di materia che la compone. Si noterebbe che un numero elevato di esse, più di 500, apparirebbe più brillante di Sirio e inoltre si renderebbero visibili molte altre stelle che in condizioni normali non lo sono.
LE SCALE SISMICHE
Esiste un altro settore del sapere scientifico che ricorre al concetto di magnitudine per quantificare l’energia che si libera in seguito ad un evento naturale: si tratta della sismologia la quale classifica i terremoti utilizzando il termine latino di “magnitudo” che, come ormai sappiamo, vuole dire grandezza.
Fin dai primordi della sismologia (dal greco seismòs che significa “scossa”) la determinazione dell’intensità di un terremoto rappresentò un problema di non facile soluzione. In un primo momento, nell’impossibilità di pervenire ad una classificazione oggettiva del fenomeno per mancanza di adeguati strumenti di misura, la forza dei terremoti veniva determinata osservando i danni che questi provocavano sulla superficie del terreno e soprattutto sulle opere realizzate dall’uomo. Questo modo di procedere era, ovviamente, molto approssimativo e legato a valutazioni personali che non potevano portare se non ad una stima sommariamente qualitativa dell’evento sismico.
Nel 1897 il sismologo italiano Giuseppe Mercalli (1850-1914) tentò di dare razionalità e universalità alla scala dei terremoti basata sugli effetti che questi producevano sulle persone, sui manufatti e sul terreno. La scala di Mercalli ebbe successo ed ancora oggi è molto usata. Essa, tuttavia, più che fornire un dato sull’intensità del terremoto fornisce una misura della gravità dei danni prodotti. Questi, come è ovvio, non dipendono solo dall’energia liberata all’ipocentro, cioè nel luogo in cui si origina il sisma, ma anche e soprattutto dalle condizioni geografico-economiche della zona colpita, nonché dal suo grado di urbanizzazione e dal tipo ed età delle costruzioni presenti.
La scala di Mercalli, all’inizio, comprendeva dieci gradi di intensità, ma successivamente fu portata a 12. L’undicesimo grado fu aggiunto dallo stesso Mercalli dopo il terremoto di Messina del 1908, mentre l’aspetto definitivo fu raggiunto nel 1956 per opera di vari sismologi. La scala di Mercalli, o come meglio attualmente viene chiamata, la “Scala di Mercalli Modificata” (scala M.M.), è di tipo empirico e pertanto priva di reale valore scientifico.
Per dare alla classificazione dei terremoti una valenza scientifica fu indispensabile trovare un sistema per misurare l’energia che si libera al momento dell’evento sismico. Allo scopo vennero sistemati, in diversi punti della superficie terrestre, strumenti adeguati in grado di registrare il fenomeno. In seguito a queste misurazioni nacque la cosiddetta “Scala delle magnitudo” ideata dal geofisico americano Charles Francis Richter nel 1935.
Gli strumenti di registrazione dei terremoti si chiamano sismografi (dal greco seismós e graphein che letteralmente significa “scrivere il terremoto”) e la registrazione che ne deriva prende il nome di sismogramma. Il principio su cui si basano i sismografi è molto semplice: si tratterebbe di costruire un supporto fisso che rimanesse fermo nello spazio mentre tutto il resto si muove sotto gli effetti della scossa tellurica. Ma questo supporto fisso, come è facile capire, è irrealizzabile e quindi si cerca di approssimare le condizioni mediante l’inerzia offerta da una massa pendolare con un periodo di oscillazione molto lungo. Quando avviene la scossa la massa molto pesante di un pendolo tende a rimanere ferma per inerzia mentre il suolo subisce un movimento brusco. In questo modo è possibile registrare lo spostamento del suolo rispetto all’oggetto che non si muove. Un elementare sismografo potrebbe quindi essere il lampadario di casa, specie se molto pesante. Apparecchi rudimentali come quello appena citato o oggetti posti in equilibrio precario pronti a cadere al minimo movimento del supporto o bacinelle piene di liquido che trabocca alla minima scossa, non sono tuttavia in grado di registrare il fenomeno, ma solo di farlo vedere: li potremmo quindi chiamare “sismoscopi”.
Un sismografo vero e proprio invece è formato da una massa metallica che viene tenuta sospesa, mediante molle o fili, all’interno di una intelaiatura in modo che risenta il meno possibile dei movimenti del terreno. Quando il telaio di sostegno viene scosso dalle onde elastiche prodotte da un terremoto, l’inerzia della massa fa sì che essa segua con ritardo il moto del telaio. Questo movimento relativo fra la massa del pendolo e il telaio che la sostiene, viene registrato da un pennino scrivente su carta avvolta intorno ad un cilindro ruotante. Il sistema scrivente non registra quindi l’effettivo movimento del suolo ma un moto molto complicato che è il risultato di due movimenti: il movimento del suolo e quello del pendolo. Sulla carta comparirà pertanto una traccia che rappresenta la copia ingrandita del movimento del suolo rispetto a quello della massa inerziale che seguirà con oscillazioni più o meno smorzate.
Il valore della magnitudo di un terremoto si determina confrontando l’ampiezza delle oscillazioni registrate dal sismografo e quella prodotta, sullo stesso strumento, da un terremoto campione. Come riferimento Richter scelse un terremoto che produce su un particolare tipo di sismografo (il sismografo a torsione di Wood-Anderson), posto a 100 km dall’epicentro (il punto della superficie terrestre posto sulla verticale dell’ipocentro), un sismogramma con oscillazione massima di un millesimo di millimetro (0,001 mm).
Supponiamo ora, per fare un esempio, di voler determinare l’intensità di un terremoto il cui epicentro, casualmente, si trovi proprio a 100 km di distanza dalla stazione di registrazione e che l’ampiezza massima delle oscillazioni che esso produce sul sismogramma sia di 0,1 mm. Il rapporto fra l’ampiezza massima del terremoto di cui si vuol conoscere l’intensità (0,1 mm) e quello standard (0,001 mm) è 100. Diremo allora che il terremoto registrato è 100 volte più “forte” di quello standard.
Quello riportato sopra è un caso limite perché abbiamo immaginato l’epicentro del terremoto proprio a 100 km di distanza e la registrazione è stata effettuata proprio dal sismografo di Wood-Anderson. Normalmente gli epicentri dei terremoti non si trovano a quella distanza dalle stazioni sismiche che tuttavia attualmente si contano a migliaia dislocate in ogni parte del globo, né i sismografi sono tutti di un unico tipo. Per poter quindi confrontare l’ampiezza di un terremoto qualsiasi con quella del terremoto standard è indispensabile calcolare il valore di quest’ultimo a distanze dall’epicentro diverse da 100 km e registrate da sismografi di altro tipo da quello preso a campione. Questi valori sono stati calcolati, una volta per tutte, tenendo conto che l’attenuazione (o l’accentuazione) delle onde che si verificano a varie distanze dalla sorgente, dipendono anche dal tipo di terreno che attraversano. Ogni stazione sismica oggi è quindi in possesso di una tabella con i valori del terremoto campione già determinati in relazione a diverse distanze, al tipo di terreno e al sismografo operante.
Poiché l’ampiezza massima di un forte sisma, registrata su un sismogramma, può essere anche milioni di volte maggiore di quella di un terremoto debole, al fine di evitare numeri molto grandi, Richter propose di ricorrere ai logaritmi di base 10. La magnitudo di un terremoto può essere quindi definita come la misura logaritmica dell’energia liberata. Il logaritmo di base 10 del rapporto fra l’ampiezza massima del terremoto misurata sul sismogramma e l’ampiezza che verrebbe prodotta dal terremoto standard alla stessa distanza rappresenta il valore della magnitudo di quel determinato evento sismico. Nell’esempio fatto in precedenza in cui il rapporto fra le ampiezze era 100, la magnitudo sarebbe stata 2. Infatti, come ben sappiamo, il logaritmo di base 10 di 100 è 2.
La magnitudo M di un terremoto può essere ricavata dalla seguente formula:
M = Log A – Log A0
dove A rappresenta l’ampiezza massima delle onde sismiche relative al terremoto considerato e A0 indica il valore massimo dell’ampiezza delle onde sismiche del terremoto campione.
I TERREMOTI PIU’ VIOLENTI
La scala della magnitudo è aperta ad entrambi gli estremi in quanto non ha un valore massimo, né minimo, e può anche assumere valori negativi. Sinora la massima magnitudo registrata è stata di poco superiore a 9 e si riferisce al terremoto che sconvolse il Cile nel maggio del 1960. Ma gli strumenti più sensibili sono in grado di registrare microsismi di magnitudo fino a –3: si tratta di scosse estremamente deboli che liberano quantità di energia insignificanti. Ad esempio un sisma di magnitudo zero libera una quantità minima di energia che, tutta insieme, sarebbe appena sufficiente per sollevare un’automobile.
Poiché la scala delle magnitudo, come abbiamo visto, è logaritmica, un aumento di un’unità nella magnitudo, corrisponde ad un aumento di un fattore 10 nell’ampiezza del movimento del terreno e ad una liberazione di energia circa 30 volte maggiore. Così, ad esempio, un terremoto di magnitudo 5 produce vibrazioni 10 volte più ampie di un terremoto di magnitudo 4 e libera una quantità di energia 30 volte maggiore di questo.
L’energia liberata da un terremoto non è derivabile direttamente dal valore di M, tuttavia esistono delle formule empiriche che consentono di correlare l’energia liberata con la magnitudo. Una di queste relazioni, che si adatta abbastanza bene per l’Italia, è la seguente:
Log E = 5 + 1,5 M
dove E è l’energia totale espressa in joule e M è la magnitudo. Un terremoto di magnitudo 6,6, come quello che si verificò in Friuli nel 1976, libera energia pari a circa 1015 joule. Questa corrisponde all’energia prodotta da 4 bombe atomiche del tipo di quelle sganciate in Giappone sulle città di Hiroshima e Nagasaki nel 1945. Le esplosioni atomiche producono molti più danni e soprattutto molte più vittime dei terremoti perché l’energia che esse liberano è concentrata su aree molto più ristrette rispetto a quelle che interessano i terremoti.
Il terremoto che colpì il Friuli nel 1976 fu, come abbiamo detto, di magnitudo 6,6, e causò 1000 morti. Il terremoto che colpì Los Angeles nove anni più tardi, nel 1985, fu della stessa magnitudo, ma determinò solo 6 vittime. I due terremoti avevano quindi la stessa magnitudo ma, rispetto alla scala Mercalli, intensità molto diverse. Come si vede non c’è corrispondenza precisa fra l’intensità di un terremoto e i valori di magnitudo in quanto i danni e le vittime di un sisma dipendono, oltre che dall’energia liberata, anche da altri fattori come il tipo di terreno su cui sorgono le costruzioni, la densità della popolazione residente e via dicendo. Se il terremoto di Messina del 28 dicembre 1908 che causò 125.000 vittime e la distruzione quasi totale della città, fosse avvenuto a qualche kilometro di distanza avrebbe risparmiato una notevolissima parte dei danni. Se poi un terremoto della stessa intensità si fosse verificato in una zona desertica, non vi sarebbero state né vittime né distruzioni e forse non sarebbe nemmeno stato menzionato dalle cronache. In un anno si registra più di un milione di terremoti (tremila al giorno) dei quali almeno dieci sono molto forti. La maggior parte di questi terremoti, fortunatamente, colpisce aree disabitate oppure ha epicentro in fondo al mare e lontano dalle coste: essi quindi non vengono avvertiti dalla gente ed ovviamente non ne viene nemmeno data notizia.
Come abbiamo già fatto notare la magnitudo è una misura strumentale del terremoto, mentre l’intensità secondo la scala Mercalli si riferisce agli effetti provocati dallo stesso e quindi non è una caratteristica di quel dato evento sismico, ma piuttosto una valutazione del modo in cui esso è avvertito nelle diverse zone della Terra. Tuttavia da un punto di vista pratico ed esplicativo è molto più significativo, per la gente comune, il riferimento ai gradi della scala Mercalli che alla magnitudo della scala Richter.
Nonostante la differenza concettuale del modo di valutare i terremoti, è ragionevole pensare che all’aumentare della magnitudo aumenti anche l’entità degli effetti. Deve esistere quindi una relazione tra magnitudo e intensità riferibile almeno alle zone abitate. Per l’Italia centro-settentrionale vale la seguente relazione empirica:
M = 0,45 I + 1,9
in cui M è la magnitudo della scala Richter e I è l’intensità massima della scala Mercalli Modificata. Il terremoto del Friuli, di magnitudo 6,6 della scala Richter, fu infatti giudicato di intensità compresa fra il X e l’XI grado della scala M.M.
I POTENZIALI DI OSSIDO-RIDUZIONE
Abbiamo visto che i logaritmi più usati sono quelli in base 10 e quelli in base e, e infatti le equazioni che descrivono fenomeni naturali attraverso l’uso di logaritmi contengono normalmente logaritmi di un tipo o dell’altro. A volte si presenta quindi la necessità di passare da un logaritmo con una certa base ad un altro con base diversa. Esiste naturalmente una formula appropriata che permette di far ciò e ci si arriva attraverso passaggi algebrici che vengono qui di seguito formulati.
Riscriviamo la definizione di logaritmo che ben conosciamo:
loga x = y
che significa:
ay = x
Scriviamo quindi il logaritmo di una generica base b dell’equazione esponenziale riprodotta sopra:
logb ay = logb x,
questa equazione, per un noto teorema sui logaritmi, diventa:
y · logb a = logb x
da cui si può ricavare il valore dell’incognita y:
logb x
y = ————
logb a
Ora, poiché, per definizione di logaritmo, sappiamo che: y = loga x, sostituendo avremo:
logb x
loga x = ————
logb a
da cui:
loga x · logb a = logb x
Nel caso di logaritmi naturali e di logaritmi decimali, sostituendo e a b e 10 ad a, la formula scritta sopra assume il seguente aspetto:
log10 x · loge10 = loge x
Ora, poiché il logaritmo in base e di 10 fa 2,303, dalla formula si ricava che per ottenere il logaritmo naturale di un numero basta moltiplicare il suo logaritmo decimale per 2,303:
loge x = 2,303 · log10 x
e quindi, con i simboli appropriati:
ℓn x = 2,303 · Log x
Una circostanza in cui si presenta la necessità di passare da un logaritmo all’altro al fine di semplificare i calcoli è quella relativa alla formula di Nernst. Si tratta di una formula che consente di determinare il potenziale di ossido-riduzione (potenziale redox) di soluzioni nelle quali le concentrazioni degli ioni presenti non sono quelle standard (1 molari).
L’equazione di Nernst normalmente appare scritta nella forma seguente:
R · T [ox]
E = E0 + ———— · ℓn ————
n · F [red]
dove E è il potenziale redox di cui si vuol determinare il valore, E0 è il corrispondente potenziale redox standard, R è la costante universale dei gas perfetti che vale, in opportune unità di misura, 8,313, T è la temperatura assoluta, n è il numero delle moli di elettroni che in seguito alla reazione si spostano da una specie chimica ad un’altra, F è il valore unitario del Faraday, cioè la carica trasportata da una mole di elettroni (che corrisponde a circa 96.500 coulomb), ℓn è il simbolo del logaritmo naturale e infine, con le scritture [ox] e [red], vengono indicate le concentrazioni molari delle specie chimiche rispettivamente allo stato ossidato e a quello ridotto.
Se si fissa la temperatura a 25 °C, cioè 298 K, che è la temperatura alla quale normalmente si opera nei laboratori scientifici, e si sostituisce questo valore nella formula insieme a quello dei termini costanti R (8,313) e F (96.500), quindi si sostituisce il logaritmo naturale ℓn con il prodotto di 2,303 per il logaritmo decimale Log, si ottiene un’espressione molto semplificata, e più facilmente memorizzabile che corrisponde a quella che viene usata in pratica:
8,313 · 298 [ox]
E = E0 + ——————— · 2,313 · Log ——— , da cui:
n · 96.500 [red]
0,059 [ox]
E = E0 + ———— · Log ———
n [red]
Vediamo ora, con un esempio, come viene usata questa formula e per quale motivo si preferisce il logaritmo in base 10 a quello in base e.
Il potenziale standard redox dell’argento E0 vale + 0,80 volt. Se invece che essere in concentrazione standard (1 molare) la soluzione che contiene gli ioni argento fosse, ad esempio, in concentrazione 0,01 molare (10-2 M), il suo potenziale sarebbe:
0,059 [Ag+]
EAg/Ag+(0,01 M) = + 0,80 + ———— · Log ————
1 [Ag]
Sostituendo i valori, e tenendo presente che la concentrazione dell’argento metallico vale 1, trattandosi della concentrazione di un solido, si ottiene:
EAg/Ag+(0,01 M) = + 0,80 + 0,059 · Log 10-2
= + 0,80 + 0,59 · (- 2)
= + 0,80 – 0,12 = + 0,68 Volt
Come si può vedere, il potenziale redox di una semipila ad argento in concentrazione 0,01 M è minore di quello relativo alla stessa semipila, ma a concentrazione 1 M. Una pila può essere quindi costruita anche unendo due semipile dello stesso elemento che differiscono soltanto per le concentrazioni degli ioni che le costituiscono. Questo tipo di pile sono dette pile a concentrazione.
IL pH
Il logaritmo più famoso che si incontra nello studio delle scienze naturali, quello di cui ha sentito parlare anche la gente comune, è senza dubbio il pH. Questo è un simbolo che si usa in chimica per indicare la maggiore o minore acidità delle soluzioni acquose.
Il pH fu introdotto, nel 1909, dal biochimico danese Søren P. L. Sørensen il quale stava affrontando alcuni problemi relativi al processo di fermentazione della birra. Questo processo richiede un controllo molto accurato dell’acidità dei mosti la quale, a quel tempo, veniva espressa attraverso la concentrazione degli ioni H+ presenti in soluzione. Questi ioni, normalmente, sono in quantità molto piccola e vengono indicati, usando le parentesi quadre per simboleggiare le concentrazioni molari, attraverso espressioni del tipo:
[H+] = 10-5 mol/L
che significa che in un litro di acqua vi è un centomillesimo di mole di ioni H+. La mole è una grandezza molto usata in chimica e corrisponde a circa seicentomila miliardi di miliardi di particelle, il famoso numero di Avogadro (6,022·1023).
Sørensen si rese immediatamente conto che i calcoli si sarebbero di molto semplificati facendo riferimento al solo esponente del valore della concentrazione, anziché a tutto il numero. Propose quindi di chiamare questo esponente pH: dove p sta per potenza (cioè esponente del 10) e H sta per idrogeno (o meglio, per ione idrogeno).
Oggi il pH viene definito come il logaritmo negativo, in base 10, della concentrazione molare degli ioni idrogeno. Pertanto:
pH = – Log [H+]
Ora, poiché il logaritmo negativo di un numero si chiama cologaritmo, possiamo anche scrivere:
pH = Colog [H+]
La conoscenza del pH riveste grande importanza sia teorica che pratica perché consente di spiegare numerose reazioni e perché dalla concentrazione idrogenionica delle soluzioni dipende la vita stessa degli organismi viventi. Ogni processo biologico e molte trasformazioni chimiche subiscono infatti profonde alterazioni per variazioni anche minime della concentrazione idrogenionica del mezzo in cui enzimi o altre sostanze devono operare. Le soluzioni acquose, in particolare, hanno bisogno di un costante controllo del pH in quanto tali soluzioni rappresentano un costituente essenziale degli organismi viventi.
L’acqua pura ha pH = 7, ma l’acqua di cui l’uomo fa uso per soddisfare le sue necessità vitali non è acqua pura, ma acqua che contiene disciolti, anche se in concentrazioni molto basse, sali ed altre sostanze che ne modificano il pH. Quando il valore del pH esce da certi limiti l’acqua non è più potabile e potrebbe anche essere dannosa oltre che per l’uomo pure per le piante e per gli animali. Il controllo del pH è quindi importante in molte lavorazioni che interessano i prodotti alimentari, i terreni e più in generale tutti quei composti chimici che l’uomo giornalmente manipola.
La misura del pH di una soluzione si può ottenere utilizzando alcune sostanze che cambiano colore a seconda della concentrazione degli ioni H+ presenti nel liquido con cui vengono a contatto. Queste sostanze sono dette indicatori chimici e non sono altro che acidi o basi deboli che si dissociano più o meno fortemente a seconda dell’ambiente nel quale si trovano. La determinazione del pH di una soluzione attraverso l’uso degli indicatori è piuttosto approssimata, ma esiste anche un modo più preciso per raggiungere lo scopo che è basato sull’uso di un apparecchio chiamato piaccametro. Questo strumento consiste sostanzialmente in una pila a concentrazione in cui un elettrodo a idrogeno è a concentrazione nota mentre l’altro è rappresentato dalla soluzione di cui si vuole determinare il pH. Dal valore del potenziale elettrico che la pila misura si può risalire alla concentrazione degli ioni H+ presenti in soluzione e quindi del pH.
LE SOLUZIONI TAMPONE
Abbiamo visto che il pH della materia vivente non può uscire da certi limiti altrimenti ne risulterebbe compromesso il procedere stesso della vita. D’altra parte gli alimenti ed altri prodotti di cui l’uomo fa uso non si conserverebbero a lungo, se non si riuscisse ad impedire la variazione del pH al loro interno. Esistono delle soluzioni particolari, dette “soluzioni tampone”, che hanno la prerogativa di mantenere grosso modo invariato il loro pH nonostante l’aggiunta di piccole quantità di acidi o di basi forti.
Una soluzione tampone si ottiene mescolando in acqua un acido debole con un suo sale (o una base debole con un suo sale) in quantità più o meno uguali. Immaginiamo allora, per fare un esempio, di voler preparare una soluzione tampone acido carbonico/bicarbonato di sodio versando in acqua uguale numero di moli di queste due sostanze fino ad ottenere un litro di soluzione.
L’acido carbonico (H2CO3) è un acido debole che in acqua normalmente è assai poco dissociato in ioni, ma, nel caso del nostro esempio, per la presenza degli ioni bicarbonato (HCO3¯), che derivano dalla dissociazione del sale e che ne impediscono ulteriormente la dissociazione, lo è ancora di meno. D’altra parte, il bicarbonato di sodio (NaHCO3), come tutti i sali, è un elettrolita forte e pertanto, in acqua, è completamente dissociato in ioni (Na+ e HCO3¯). In soluzione, trascurando gli ioni Na+ che non ci interessano, si viene quindi ad instaurare l’equilibrio seguente:
H2CO3 ⇄ H+ + HCO3¯
in cui le molecole di acido indissociato sono presenti in numero più o meno uguale a quello degli ioni bicarbonato (una mole per entrambi). La costante di equilibrio dell’acido carbonico (Ka) è data dalla seguente espressione:
[H+] · [HCO3¯]
———————— = Ka
[H2CO3]
che può essere scritta, in seguito a facili passaggi, anche nel modo seguente:
1 1 [HCO3¯]
——— = —— · —————
[H+] Ka [H2CO3]
quindi, passando ai logaritmi in base 10, abbiamo:
1 1 [HCO3¯]
Log ——— = Log (—— · —————)
[H+] Ka [H2CO3]
Il logaritmo di 1/[H+] non è nient’altro che il pH, infatti, per un noto teorema che abbiamo già incontrato in precedenza, il logaritmo del quoziente di due numeri positivi è uguale alla differenza fra il logaritmo del dividendo e quello del divisore; possiamo quindi scrivere:
1
Log ——— = Log 1 – Log [H+] = – Log [H+]
[H+]
perché il logaritmo in base 10 di 1 è 0. Ora, poiché abbiamo definito:
pH = – Log [H+],
deve valere anche
1
pH = Log ———
[H+]
Per analogia con pH, il logaritmo decimale dell’inverso della costante di acidità (Log 1/Ka) di un acido debole viene indicato con pKa, pertanto l’equazione scritta sopra ora prende la forma seguente:
[HCO3¯]
pH = pKa + Log —————
[H2CO3]
Questa espressione è detta equazione di Henderson e Hasselbach e rappresenta un’altra delle tante equazioni, che si possono incontrare nello studio delle scienze naturali, nelle quali compaiono i logaritmi.
La Ka dell’acido carbonico vale 4,3 ·10-7 mol/L e pertanto il pKa cioè il logaritmo cambiato di segno di quel numero, vale 6,37. Se la concentrazione dell’acido carbonico e del suo sale (che coincide con quello degli ioni HCO3¯) sono le stesse, il loro rapporto sarà uguale a 1. Il logaritmo di base 10 di 1 fa 0: ciò significa che il pH di una soluzione siffatta è uguale al pKa dell’acido che è stato adoperato per realizzarla, cioè, nel nostro caso, a 6,37. Un sistema tampone funziona nel modo migliore quando il suo pH è uguale al pKa dell’acido che è stato adoperato per prepararlo.
Vediamo ora per quale motivo un sistema tampone “tampona”, cioè per quale motivo una tale soluzione non fa sentire i suoi effetti quando in essa vengono aggiunte piccole quantità di acido o di base anche forti.
Per rispondere a questa domanda immaginiamo di aver preparato un litro di soluzione tampone mescolando una mole di acido carbonico e una mole di bicarbonato di sodio in acqua. Il pH della soluzione sarà 6,37 e in questa soluzione vi sarà praticamente lo stesso numero di molecole di acido e di ioni HCO3¯. Supponiamo ora di versare in questa soluzione una piccola quantità di idrossido di sodio (NaOH), per esempio un millesimo di mole (4 centesimi di grammo, una quantità piccolissima). L’idrossido di sodio è una base forte che in soluzione libererà immediatamente tutti gli OH¯ di cui dispongono le sue molecole. Questi si uniranno agli ioni H+ che l’acido debole metterà a disposizione perché indotto a dissociarsi ulteriormente proprio dalla la presenza degli OH¯, formando molecole di acqua indissociate. Gli ioni OH¯ spariranno quindi dalla soluzione, ma nello stesso tempo calerà il numero delle molecole di acido (per avere fornito gli H+) e aumenterà quella degli ioni bicarbonato. La differenza, rispetto alla situazione iniziale, sarà però minima e quindi lascerà praticamente invariato il valore del logaritmo che compare nell’equazione di Henderson e Hasselbach: il pH della soluzione rimarrà praticamente lo stesso (6,37). Per confronto si consideri che se la stessa quantità di idrossido di sodio (0,001 moli) venisse versata in un litro di acqua pura, invece che nella soluzione tampone, l’acqua cambierebbe il suo pH da 7 a 11, con un salto di ben 4 unità.
Lo stesso evento, ma di natura opposta, si verificherebbe aggiungendo una piccola quantità di un acido forte, per esempio 0,001 moli di HCl. In questo caso gli ioni H+ derivati dall’acido forte che si liberano in soluzione andrebbero a legarsi agli ioni bicarbonato formando molecole indissociate di acido carbonico e facendo quindi sparire dalla soluzione gli ioni responsabili dell’acidità. Nel contempo diminuirebbe però il numero degli ioni bicarbonato mentre aumenterebbe quello delle molecole di acido, ma la differenza rispetto alla situazione iniziale sarebbe minima, tanto che il valore del logaritmo all’interno della equazione di Henderson e Hasselbach rimarrebbe ancora una volta praticamente invariato e quindi nemmeno il pH cambierebbe di molto.
Il pH del sangue si mantiene intorno al valore di 7,4 nonostante l’aggiunta o la sottrazione di prodotti metabolici che tenderebbero a farlo variare. Per poter mantenere costante il suo pH il sangue utilizza alcuni sistemi tampone il primo dei quali è basato sulla presenza dell’acido carbonico e dello ione bicarbonato. L’acido carbonico, presente nel sangue e nei fluidi extracellulari, è a sua volta in equilibrio con la CO2 che si forma in seguito al metabolismo cellulare. La reazione di equilibrio fra anidride carbonica ed acqua che porta alla formazione dell’acido carbonico è la seguente:
CO2 + H2O ⇄ H2CO3 .
Quando l’acido carbonico si dissocia per liberare ioni H+ al fine di tamponare gli OH¯ che sono stati aggiunti, altro acido carbonico si forma a spese dell’anidride carbonica che non viene quindi espulsa attraverso la respirazione. Viceversa quando si forma troppo acido carbonico in seguito alla presenza, nei liquidi interstiziali, di acidi di varia provenienza, la quantità sovrabbondante si scinde in anidride carbonica ed acqua, sostanze che poi verranno eliminate attraverso la respirazione.
Prof. Antonio Vecchia



Complimenti, bellissimo articolo!